Concerning [an integral] and a Taylor series method
33. R. S. Anderssen, R. P. Brent, D. J. Daley and P. A. P. Moran,
Concerning
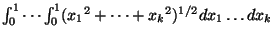 and a Taylor series method,
SIAM J. Applied Mathematics 30 (1976), 22-30.
MR 52#15773.
and a Taylor series method,
SIAM J. Applied Mathematics 30 (1976), 22-30.
MR 52#15773.
Abstract:
dvi (3K),
pdf (81K).
Paper:
pdf (648K).
Abstract
The integral of the title equals the mean distance
mk from the origin
of a point uniformly distributed over the k-dimensional
unit hypercube Ik.
Closed form expressions are given for
k = 1, 2 and 3,
while for general k,
mk is asymptotic to
(k/3)1/2.
Using inter alia methods from geometry,
Cauchy-Schwarz inequalities
and Taylor series expansions, several inequalities and an asymptotic series
for mk are established.
The Taylor series method also yields a slowly
converging infinite series for mk
and can be applied to more general
problems including the mean distance between two points independently
distributed at random in Ik.
Comments
For recent references, see the MathWorld
"Hypercube Line Picking" page.
Go to next publication
Return to Richard Brent's index page