

Figure 1. This was the frontpiece to Novum Organum (perhaps The New Methodology), in which Francis Bacon (1561-1626) set out proposals for a systematic approach to scientific discovery. The ship is sailing through the Straights of Gibraltar, out beyond the common limits of exploration for English ships at that time. Bacon looked for a new era of scientific discovery where the old boundaries and the old ways of thinking would no longer constrain discovery. Contrast Bacon's metaphor of exploration at sea with the data mining imagery of exploration under the earth's surface.
Data mining is the data analysis component of Knowledge Discovery in Databases (KDD). According to its exponents, KDD encompasses all steps from the collection and management of data through to data analysis. Frequent themes are analysis (both exploratory and formal), methods for handling the computations, and automation, all with a focus on large data sets. At a superficial level, any data set is large where there is a large number of observations, perhaps running into the millions or beyond. Such data sets do pose challenging database management and computational problems but are not necessarily large for predictive purposes, where it is essential to have regard to the data structure. Thus a survey of the use of fax machines in Australian might gather huge amounts of data from just six universities, making prediction to Australian universities as a whole hazardous. In addition or alternative to structure of this type in the sampling units, there may be extensive sampling over time. A further issue is homogeneity. A predictive spatial model which works well for areas where vegetation is sparse, perhaps inferring soil characteristics from satellite imaging data, is unlikely to work well for heavily forested areas.
Data structure affects the forms of graphical or other summary that are appropriate. It often has strong implications for obtaining realistic assessments of predictive accuracy, whether theoretically based or using cross-validation or using the training/test set methodology. In both cross-validation and in the use of the training/test set methodology, data structure and the intended use of any predictive model may be relevant to the division of the data between training and test set. Data structure has implications for data analysis and for efficient modelling.
Data sets which are relatively large and homogeneous, to the extent that it might be reasonable to use mainstream statistical techniques on the whole or a very large subset of the data, raise at least two types of issues for practical analysis. Algorithms that work well with data sets of modest size may fail or take an unreasonably long time to run in really large data sets. Inferential procedures, including cross-validation and the training/test set methodology, may suggest that estimates are more accurate than is really the case. There are at least two reasons for this: (1) various forms of dependence are almost inevitably present in any large data set and may be difficult to model adequately, and (2) the data are almost never a random sample from the context to which results will be applied. Point 1 has special relevance to mainstream model-based methods of assessment of predictive power. Point 2 emphasises the importance of validating any predictive model under the conditions of its intended use.
The collection of data together into large databases raises further issues. Such collections may and often should be the basis for data-based overview of a whole area of knowledge, allowing for much better and more informed use of research-based knowledge and more informed planning of future research. Evidence from such databases must be used critically, having regard to the widely differing quality of different types of evidence. These points are well illustrated from experience with medical databases.
Even where the initially collected data are of high evidential quality, distortions may be introduced by the processing of the data for publication. On the one hand, forms of summarisation which do not lose information in the data can make later use of the data much easier. On the other hand, cavalier summary analysis, including some statistical analyses which form the basis for results that are presented in journals, have the potential to introduce serious and unacceptable biases. Example are given. Data quality issues take a variety of forms. The retention of crucial background information, including information on data structure and potential sources of bias, is a key issue for the collection of data together into databases.
Exploratory data analysis must, for large data sets, rely heavily on various forms of data summary. What forms of data summary are likely to be helpful, while losing minimum information from the data? It may often be reasonable to base analyses on one or more random samples of the data. Where data cleaning is a large chore, there may be a trade-off between time spent on data cleaning and time spent on analysis. It may then make sense to limit cleaning to a random sample of the data, allowing more time for analysis.
Data mining, statistics, data analysis, knowledge discovery in databases, evidence-based medicine, Francis Bacon.
"Data mining" and the allied term "Knowledge Discovery in Databases" (KDD) are in the tradition of "artificial intelligence", "expert systems", and other such terms which computer technology regularly spawns. Knowledge Discovery in Databases gives a better sense of the aims of the enterprise than the term "data mining". We have databases, often quite large databases, and we want information from them. The search may or may not follow a highly structured pattern. What matters is that knowledge comes out at the end.
Data mining is a brash metaphor that is designed to grab attention, much as the `voyage of discovery' image in Figure 1 was designed to grab attention. Bacon, like modern data miners, wanted to sell an idea. Bacon was the first great advocate of organised scientific research. Bacon wanted a research institute The College of the Six Days' Works created to systematically gather and systematise all knowledge. In Bacon's fictional New Atlantis, this becomes Salomon's House.
I will define statistics as the science of collecting, analysing and presenting data. If this admittedly broad definition is accepted, then KDD is statistics and data mining is statistical analysis. KDD has a spin that comes from database methodology and from computing with large data sets, while statistics has an emphasis that comes from mathematical statistics, from computing with small data sets, and from practical statistical analysis with small data sets. People whose forte is practical data analysis are not as much to the fore as they should be in either community. The best results will come from a merging of the insights and skills of those who come from diverse intellectual traditions.
The points I make will be illustrated using quite small data sets, which are tractable for the purposes of this paper. Large data sets raise these same issues, and other issues besides. I will emphasise that large data sets often contain, for the purposes for which the data will be used, a relatively small number of independent items of information. This is important when considering whether the huge extent of a data set may allow the use of analysis methods which, for small or medium sized samples, would make very poor use of the data.
All analyses, whether those of mainstream statistics or those favoured by data miners, have as their intended outcome the reduction of a set of data to a small amount of readily assimilated information. The forms of summary may include graphs, or summary statistics, or equations that can be used for prediction, or a decision tree. Often it is helpful to carry out this process of summarisation in several steps. Where a large volume of data can without loss of information be reduced to a much smaller summary form, this can enormously aid the subsequent analysis task. It becomes much easier to make graphical and other checks that give the analyst assurance that predictive models or other analysis outcomes are meaningful and valid. Relevant graphical summaries are perhaps the most important tool at the data analyst's disposal. Experimentation with alternative forms of graphical representation becomes far more feasible once the data have been reduced to managable size. Data structure is the key to data summarisation, and will be a large focus of this paper.
What sorts of databases are we talking about? Here are some examples.
At Australian National University there has been work on huge astronomical data sets. The Massive Astronomical Complex Halo Object (MACHO) database (Ng et al., 1998) has time series from about 20 million stars, collected from each star for a period of four years. This is being searched for evidence of massive compact halo objects.
In items 3 and 4, the data quality, data relevance, data collection and data analysis issues that I have highlighted are likely to be very troublesome.
Expositions of data mining suggest widely varying ideas of the aims of data mining. Elements which may be present include:
My own story of serendipity concerns an experiment (Maindonald and Finch 1986) to determine whether trucks with mechanical suspension are kinder to apples than trucks with airbag suspension. The data had outliers which surprised us. Investigation revealed occasional unstable bins where there were huge levels of damage, dwarfing any effect from suspension. It was not at all the result we were looking for. In retrospect we ought to have looked carefully at the bins that we intended to use. A modicum of careful experimental design was crucial to this finding.
Highly automated analyses do not create the conditions for serendipity. We have not yet learned how to construct computers so that they have the "Aha" experience. Serendipity does not go well with the passion for automation.
Exploratory data analysis can be simple-minded, for example using normal probability plots to look for outliers in columns of data. Or it may be very sophisticated. Where careful data analysis has been something of an oddity, simple-minded exploratory techniques may yield easy results. The striking differences in hysterectomy rates between New England and Norway which McPherson et al. (1982) found would have been obvious even to a casual observer. In the study of comparative mortality rates in coronary artery bypass grafting that is reported in Chassin et al. (1996), comparisons were not totally straightforward. Adjustments for prior risk were needed to give figures that were genuinely comparable. Again, there were some large effects. 27 surgeons who each performed less than 50 operations had, for the part of the period 1989-1992 for which they practiced, an average risk-adjusted mortality rate of 11.9% as against a statewide average of 3.1%. In the last of the five years for which results are reported, data was from a total of 16,690 patients.
The search for particular kinds of interesting objects might, as Alan Welsh has suggested, be called "data prospecting". Prospectors have a clear idea of what is valuable and what is not. There's structure in their searching. An example is the search for interesting features in the MACHO data set (Ng et al.). One needs a very sophisticated form of exploratory data analysis. Simple forms of searching will not reveal anything. Mackinnon and Glick (1999) suggest the term "data geologist".
Finally, there are classification and regression problems. Based on events that have been associated with earlier computer incursions (or break-ins), computer administrators want to be able to detect the tell-tale signs of any new incursion. Or a marketing firm may want to predict which potential addressees are likely to respond. In hot spot analysis the aim is to find addressees who are highly likely to respond.
Here I will demonstrate a data set of modest size which reduces, for some predictive modelling purposes, to just six independent items of information. The same often happens when there are much larger datasets. Consider for example a hypothetical study of the use of fax machines in large organisations. It will be much easier to get extensive information from a small number of obliging organisations, than to get information that is widely representative of large organisations.
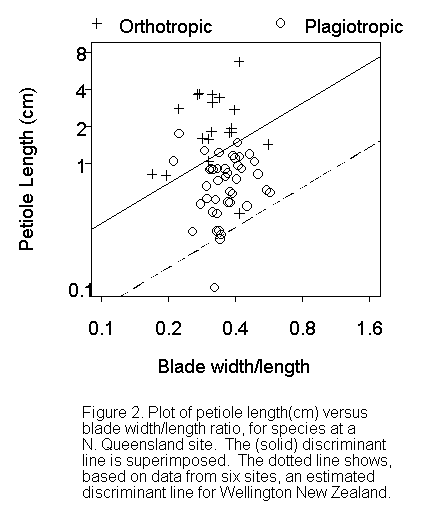 The data consists of 286 observations drawn from six sites at a variety of latitudes. For purposes of generalising to other comparable sites we have, effectively, six observations. The example is, like many of the examples in books on data mining and machine learning, is a classification problem. It comes from a study of geographical variation in plant architecture (King and Maindonald 1999). Orthotropic species have steeply angled branches, with leaves coming off on all sides. Plagiotropic species have spreading branches. David King was interested in comparing the leaf dimensions of the two types of species.
The data consists of 286 observations drawn from six sites at a variety of latitudes. For purposes of generalising to other comparable sites we have, effectively, six observations. The example is, like many of the examples in books on data mining and machine learning, is a classification problem. It comes from a study of geographical variation in plant architecture (King and Maindonald 1999). Orthotropic species have steeply angled branches, with leaves coming off on all sides. Plagiotropic species have spreading branches. David King was interested in comparing the leaf dimensions of the two types of species.
It turns out that, at each of the locations, one can discriminate between orthotropic and plagiotropic, based on two quantities, the leaf width to length ratio, and the petiole or leaf stalk length. Figure 2 shows the plot of the data, together with discriminant line, for North Queensland. Different latitudes require different lines. The line moves up for locations that are closer to the equator, and down for locations that are further from the equator. The dotted line, on the same graph, shows my prediction for Wellington. The line has the same slope, only now it has shifted down. It is then fair to ask: "How accurate is the discrimination?"
For another sample of plants from the same six sites, the estimated accuracy of prediction is 87.4%. One gets this by cross-validation here I divided the data up into ten parts, then left out each 10% of the data in turn and predicted the classification for the omitted 10% from the data that are left in.
But Wellington is not one of the original six sites. I have assumed that the whole of the difference between the six sites is explained by latitude differences. That may not be true. There are a number of other variables which may be important: altitude, temperature, cloud cover, rainfall, and so on. With our present data these other variables are not needed to explain differences between the six sites. Nevertheless, in data from a wider range of sites, some of them may turn out to be important. To get a fairer estimate of the accuracy of prediction at some new site one needs to leave out sites one at a time, and use the remaining five sites for prediction. I had expected that the estimated accuracy of prediction would deteriorate badly. It turns out it does not change much, which may be just luck. Note also that with just six sites the estimate of prediction accuracy is itself inaccurate. Saying that we have 286 species sounds pretty good. Noting that we have only six sites spoils the story.
We are still talking about estimates of accuracy that are internal to these data. The sites were not selected at random. If we had sites in abundance we might separate the data into two parts, using one set of sites to develop our model and another set to test it out. I would then be relatively well placed to comment on the accuracy of prediction of the discriminant line that I have drawn for Wellington.
If we had huge amounts of data we might use the training/test set idea. There are two possibilities. We can either split the data from each site into two parts, or we can assign a proportion of the sites to the training set and the remainder to the test set. Here is the first possibility.
| Site 1 | Site 2 | . | Site 60 | |
| Training set | 60% | 60% | 60% | |
| Test set | 40% | 40% | 40% |
The other possibility is:
| Training Set | Test Set |
| 30 Sites | Remaining Sites |
The training/test set idea safeguards against an inappropriate model, but only if the test set reflects the structure of the population to which predictions will be applied. Thus the second of these ways of dividing up the data is required, to be able to generalize sensibly beyond the sites that were used in the sample. Note however that we still have only an internal measure of accuracy, from purposively chosen sites. To get an external measure of accuracy we need to choose totally new sites and see how well the predictive model performs on them.
In summary, there are several points which emerge. However much information had been gathered from the North Queensland site, it could never have told us about the effect of latitude. For puposes of giving information on the effects of latitude, data from the Queensland consisted of one item of information only. Even when we take all data together, the whole data set has only six independent items of information on the effects of latitude. No matter how much further information we might gather from these six sites, this limitation would remain. Even with six sites there are other variables whose effects we cannot assess. One such pertinent variable may be altitude.
The idea of training set and test set is of enormous importance. The training data set is used to develop the model. The test set is used to check the accuracy of model predictions. So also are the structure of the training sets and test sets. We need to tell first year statistics students about training sets and test sets. Cross-validation may be seen as an extension of the training/test set idea. It uses all the data for prediction, while giving the same insight on the accuracy of predictions that is available from the training/test set methodology.
Detection of computer intrusions provides another example. Here we are clearly dealing with a moving target. Any accuracy rate that is based on the training sample will be optimistic. The intruders will have honed their methods, effectively changing the target population, by the time that we come to use the discriminant function. We might choose the training set to be data for the first six months, and the test set to be data for the next three months. Or one might split the original data into training and test set for purposes of developing the model, then using a validation set consisting of new data for testing the model. Validation should be a continuing ongoing process, as new data accumulate.
Statisticians like to build models and use the model both to make predictions and assess the accuracy of the predictions. Again I will use a small and tractable data set to illustrate points which have equal relevance to large data sets. I use it to highlight the common importance of the time dimension.
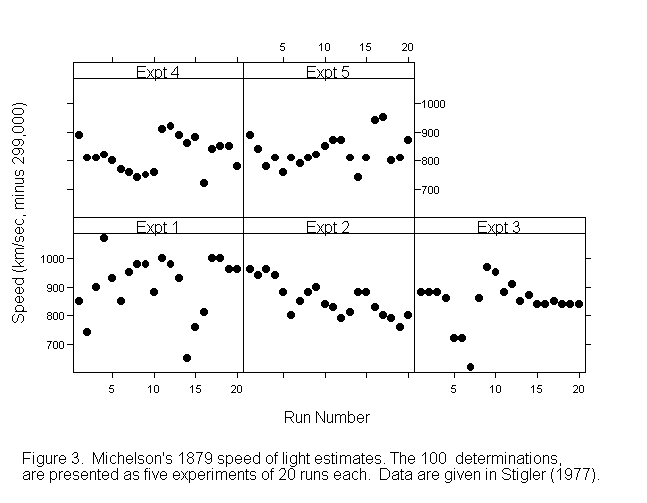 The data in Figure 3 are from a series of experiments which Michelson conducted in 1879 to measure the speed of light. There is clear correlation between the result from one run and the result from the next, but with an occasional sudden change. A consequence is that the estimate from two points that are close together in time are much more similar than the results from points that are well separated.
The data in Figure 3 are from a series of experiments which Michelson conducted in 1879 to measure the speed of light. There is clear correlation between the result from one run and the result from the next, but with an occasional sudden change. A consequence is that the estimate from two points that are close together in time are much more similar than the results from points that are well separated.
In order to make inferences for these data we require a model that allows for this serial correlation. For example, we may wish to ask whether there are systematic trends, up or down, within each experiment. Or is the apparent pattern a result of the serial correlation? Our argument may rely quite heavily on the model assumptions. There are several possible reasons for building a model that allows for the sequential correlation. One is to get an efficient estimate of the slopes. Another is to allow us to get reliable estimates of model accuracy. If in Figure 3 we had huge numbers of slope estimates we could for these purposes reduce or avoid reliance on modeling of the sequential correlation structure in each run. A third reason is that we may wish to understand why each result is so strongly influenced by immediately previous results. How far back in the sequence does this influence go?
Much of the bulk of some of the largest databases is a result of intensive sampling over time. Mackinnon and Glick note that the Earth Observing System (EOS) satellites will generate around 0.33× 1015 bytes of data in a year. There must be attention to time dependence.
| Small Data Sets | Medium Size | Large Data Sets | |
| Need for efficient prediction? What model structure is desirable? |
Strong Linear terms |
Reduced Smoothing terms can be fitted |
Much reduced. Decision trees may be acceptable. |
| How can we get internal estimates of accuracy? (i. e. prediction to a similarly drawn sample) |
Estimates must be model-based, with strong assumptions | Alternatives are: model-based estimates, or use resampling, or training/test sets | Use training/test set, with random splitting of the data. |
| How can we get external estimates of accuracy? (i. e. prediction outside of sample population) |
No good alternative to reliance on model-based assessments | Use training/test set, with purposive choice of test set. | Use training/test set, with purposive choice of test set. |
| Table 1. An assessment of how size of data set may effect model prediction and assessments of the accuracy of estimates. | |||
Table 1 gives a broad assessment of the implications of size of data set for the sorts of reliance that we must or can afford to place on models. We are forced to make strong assumptions in order to get anything useful from small data sets. With data sets that are genuinely large, assumptions such as linearity that are inevitable in a small data set may unacceptably bias the more accurate predictions that are now possible. Our predictions are often reasonable, while our estimates of accuracy may very often be problematic. With very large data sets we can afford to use methods, of which the simpler types of decision tree methods seem the most popular, which do not take advantage of important features of much of the data on which they are used. We can at the same time afford to base our analysis on a part only of the data, keeping the rest for testing predictive accuracy. Estimates of accuracy obtained in this way are in general safer than model-based estimates of accuracy.
Data sets that are genuinely large, in the sense that they have a huge amount of replication at the level of what survey statisticians call the primary sampling unit, are much rarer than is commonly supposed. While the number of patients in the data on mortality from heart surgery that we considered earlier was of the order of 70,000, the number of surgeons would have been less than 200, still more than enough for a study of factors which may affect differences in mortality between one surgeon and another.
With data sets that are genuinely large, heterogeneity may become a problem. Satellite imaging data may be able to predict soil characteristics fairly well over homogenous areas where there is little ground cover. Models developed for making predictions in this simple case will nor generalise to handle areas covered by forest or scrub, or where there are marked changes in the landscape. To develop models that will be effective, one needs large amounts of data for each different type of terrain, widely sampled over that terrain. The task is further complicated because the pattern of spatial dependence will change from one type of terrain to another. Data sets that are large enough for developing predictive models that can cope effectively with these different types of heterogeneity are unusual.
The possible or probable extent of heterogeneity will vary from one type of study to another. The pattern of responses of human populations to medical treatment seem likely to remain broadly similar as one moves to from one location to another. Television advertising seems to work in much the same way in Beijing as in Sydney. There is much less need to worry about the huge heterogeneities, both in the pattern of response and in the correlation structure, that one finds in spatial data.
Statisticians will do well to be sceptical about model-based and other internal estimates of error. Those from a data mining perspective need to understand the importance of data structure both for getting efficient estimates and for assessing predictive accuracy. Not every huge collection of numbers has large numbers of independent items of information, at the level of variation that is important. The computer intrusions example illustrates the frequent demand for an external check on accuracy.
There are several alternatives:
Finally, there may be merit in sampling from very large data sets, using the sample for exploratory analysis and perhaps even for the final analysis. This makes especial sense when data cleaning is a huge chore, and there is a trade-off between time spent on data cleaning and time spent on analysis. Restriction of the cleaning to a sample may give large time savings, allowing more time or resources for data analysis. Uthurusamy (in Fayyad 1997) comments that "It is better to prevent than process the data glut." This is where statistical input may be very important. Checks which remain possible when data are collated may be impossible later. Some aggregation of information at the collection stage may enormously ease the later processing task. Collecting information on every variable in sight is not a good idea, unless these variables are ranked for relevance and importance.
It is however important not to lose key background information. One should not rely on forms of summary which are known to, or may, introduce serious distortions. An example will appear later. Background information that must be preserved includes:
Statistics, as I want to define it, is the science of collecting, organizing, analysing and presenting data. "Knowledge Discovery in Databases" is not much different. The components that seem needed are:
Data mining and statistics have different intellectual traditions. Both tackle problems of data collection and analysis. Data mining has very recent origins. It is in the tradition of artificial intelligence, machine learning, management information systems and database methodology. It typically works with large data sets. Statistics has a much longer tradition. It has favoured probabilistic models, and has been accustomed to work with relatively small data sets. Both traditions use computing tools, but often different tools. Data mining may now be entering a less brash and more reflective phase of development, where it is more willing to draw from the statistical tradition of experience with data analysis. Efron's warning is apt:
Many statisticians of my generation went immediately from a training in mathematics to the practice of statistics. We learned statistical tools, slowly and going too frequently down blind alleys, as we went along. We now see a partial replay of this history, in the context of large data sets. Skills in the manipulation of large databases are necessary to do anything at all. It will take time to get widespread acknowledgement that the skills and tools needed to manipulate large data sets may not, on their own, be enough.
In important respects, data mining is in the tradition of artificial intelligence. There is the same temptation to make outrageous promises. The term Artificial Intelligence seems now fallen in disrepute. Here are the words of one pioneer in the area, speaking in retrospect:
We are still a long way from a viable automated approach to data analysis, whether for small or for large data sets. It is often a considerable effort for competent data analysis professionals to get data analysis software to provide an enlightened and meaningful analysis. Many aspects of the computations that can and should be automated are not. Or the desired output information may be almost impossible to get with current software. While there are serious limitations in the data analysis software that would be at the heart of any automated system, what hope is there for a mechanically driven process?
Until recently the predominant commercial data mining tool for predictive modelling was one or other version of decision trees. There has been some use of logistic regression, some use of classical regression methods, and some use of neural nets. Broadly, data miners are likely to use one or other decision tree method as their tool of first recourse, while those from a statistical tradition use a broad range of tools which may or may not include decision trees.
Decision trees do not work well with small data sets. One reason is that they take only limited advantage of the ordering relations and continuity notions that are implicit for continuous variables. This loss of information may not be serious when there is so much data that one can afford to jettison much of the information that it contains. The advantage of decision trees is that they place little constraint on the pattern of relationship. Neural nets offer the same kind of flexibility that is available from a smorgasboard of mainstream statistical models. The user must make a choice from the huge range of nets that is available. At the same time, there is a very limited tradition of experience on which to draw when choosing between the nets that are on offer. Perhaps the best commentary is Ripley (1996). Most statisticians prefer, for the time being, to stay with tools where the choices are better understood and where the output can be expressed in the form of graphs and/or equations. (The graphs I have in mind is graphs that are a representation of a functional form.)
Recent work by Jerome Friedman and others offers interesting new methodologies that build on a decision tree approach. At the very least tree-based methodologies provide a useful exploratory tool to use when starting investigation of data sets which, even allowing for whatever structure may be present, are large. They may quickly highlight major features of the data that are important for predictive modelling. They provide useful clues for subsequent more careful modelling using methods where the predictive model can be expressed in graphical and/or equation form.
At best, the collection of data together into databases creates a resource which researchers can use in constructing an accounts that use all the data. At worst, such databases may suffer from some or more of the deficiencies: they may contain serious errors, there may be biases that arise from collection or from prior processing, key background information may be missing, information on key variables may be missing, high quality information may be mixed with information that is of very poor quality with few clues that will allow the researcher to distinguish. Here I provide examples that illustrate some of these points.
There is now a large body of experience, in selected areas of research, with the data relevance and quality issues that arise in the use of evidence from databases. My concern here is to draw attention to the experience of of clinical medicine . Data relevance and quality issues are important both for the collecting together of data, and for its analysis. Particularly relevant is the experience of the emerging tradition of "Evidence-Based Medicine" (EBM; see for example Sackett et al. 1997) seems. This tradition, and clinical medicine generally, has had extensive experience in trying to pull together evidence from multiple sources. Much of the EBM activity goes on under an umbrella organisation called the "Cochrane Collaboration" (Sackett and Oxman1994). All data analysts can learn from what EBM and the Cochrane Collaboration have made of Francis Bacon's ideas.
The Cochrane Collaboration exercises, with their emphasis on data-based overview of major medical issues, have strong connections with Knowledge Discovery in Databases. The best assessment of the evidence will come from a careful critical assessment that is based on all the data. Results in individual scientific papers or from one groups of researchers can, taken in isolation, be quite misleading. Were this point better understood and acted on, there would be large implications for many areas of scientific research. There would be a strong focus on data-based critical overview. Contributing to such overviews, data which have formed the basis of published results would be archived. Knowledge discovery in databases is a great idea, but it will not be easy to set in place the mechanisms that will make it effective for its intended purpose.
The relatively small extent of the databases used for Cochrane Collaboration exercises makes no difference to the principles that apply. Such exercises make a virtue of the fact that, for example, numerous researchers in different parts of the world have done trials on the use of aspirin to ward off heart attacks. The different trials are in effect replications of a similar experiment, even though there has not been any large element of common planning. If a result can be replicated over half a dozen clinical trials, there is a good chance that it may be reproduced in clinical practice.
Evidence-based medicine is not primarily focused towards research, but towards ensuring that research results are assimilated into clinical practice. There are however huge implications for research. Some of the key insights are:
There is a continuing debate over whether salt has a major role in causing hypertension high blood pressure in the populace at large. The present state of the debate was summarised in an article (Taubes 1998), called "The (Political) Science of Salt", that appeared last August in Science. Different observational studies give different answers. Randomised clinical trials indicate that any effect is very small, certainly not large enough to justify a huge expenditure of public funds on efforts to reduce salt consumption. I believe the clinical trials. Huge amounts of public money have been wasted because of reliance on data that was incapable of providing the answers that were sought. There has also been a reliance on animal models that were relevant, if at all, only to patients already suffering from hypertension. Specifically, one early researcher into the effects of salt had been able to breed a strain of salt-sensitive hypertensive rats. This was taken as evidence that it was bad for humans to eat salt.
Researchers as well as clinicians need the information that EBM tries to provide. Researchers need it so that they can get a good sense of what is already known, so that they can identify knowledge gaps, and so that they can avoid the mistakes of earlier workers. They also need it because published research gives a biased and incomplete coverage of the trials that have been undertaken, with negative results often sitting in a drawer unpublished. Trying to get around that problem is a task for a team of experts.
It should not be so hard. There is a need for an international register of clinical trials, and to archive data from trials under arrangements that guarantee anonymity. It is then available for later overview studies, or for re-analysis if there are suspicions about the initial analyis. Finally, there needs to be a high standard of reporting, so that anyone doing an overview study can easily verify, for example, whether the allocation of treatments was indeed randomised. This has led to a set of reporting standards, set out in the Consort statement (Begg et al. 1996).
Here however, my interest is in implications for the creation and use of data from databases. Care, scrutiny and critical evaluation are required at every step. Not all sources of evidence are of equal value. It is important to distinguish what is potentially misleading from what is soundly based.
There are proper and necessary roles for observational databases. Mackinnon and Glick (1999) refer to a New York Times report (Kolata 1997) that the US Food and drug Administration wants a database to monitor about 200,000 reports per year of adverse drug reactions. Such a database would seem long overdue. Drug trials cannot investigate the whole range of circumstances that will occur in clinical practice. Data collection and data analysis will often be ongoing, rather than providing an authoritative analysis at a particular endpoint in time. Many commercial applications have this character. Fraud detection is an obvious example.
Even where the initially collected data are of acceptable quality, distortions may be introduced by the processing of the
 data for publication. This leads to distortions when processed data, taken from published papers, is collected into databases.
data for publication. This leads to distortions when processed data, taken from published papers, is collected into databases.
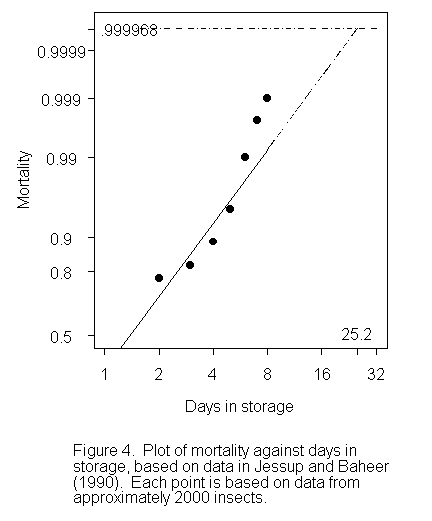
Figure 4 presents another example, this time from work on killing insects in produce that may be intended for export. The graph presents data, and the results of analysis, that appeared in a paper (Jessup and Baheer 1990) in the Journal of Economic Entomology. A commonly used transformation, the probit, has been used on the vertical scale. There are two problems. (1) The author has extrapolating well beyond the limits of the data. (2) The line does not fit the data.
Jessup and Baheer did at least present their data. Many of the authors who present results in the Journal of Economic Entomology do not. All they give is a line. So when one sees figures such as appear in Table 2 below, it is impossible to know whether they are comparable. The calculations that gave the New Caledonia value are mine (Sales et al. 1997), and used a complementary log-log model. The Queensland figure is from Heard et al. (1989), and assumed a probit model. My suspicion is that it is affected by a bias which is similar to, though less extreme than, that in Figure 4.
|
|
New Caledonia | Queensland |
| Third Instar of Queensland Fruit Fly | 8.4 min (95% CI: 7.7 - 9.3) |
11.6 min |
| Table 2. Estimated times to 99% mortality, following immersion in hot water at 47°C. | ||
An obvious database construction exercise is to go through the Journal of Economic Entomology and pick out information e. g. on 99% mortality points where they are available. It is not, in most cases, possible to go back to the original data. Clearly, given the unreliability of the analyses, the databases should be storing the original data, not the estimates of the 99% mortality point or other results from analyses. The bad news is that the original data are rarely likely to be available. Posterity would be better served if all those authors who have published in the Journal of Economic Entomology had drawn a curve through their data by eye. One may hope that the current passion for putting data together into databases will highlight the huge problems that our inattention to such matters is creating for the future use of the results of much current scientific work.
Environment Australia and others are putting a huge effort into collecting together data that will give information on species abundance and distribution. There are various kinds and qualities of data data collected haphazardly for taxonomic purposes, data collected from carefully chosen sites, data that uses statistical sampling approaches to assess biodiversity over a wide area, and predictions that are based on fitting models to data of any or all of the forgoing types. These mirror the clinical medical contrast between the different types of observational data and varying standards of clinical trials. Different types of data are not all of equal value or quality. Some data turn out to be totally useless for their claimed purpose. If garbage goes in, garbage is certain to come out.
Elder and Pregibon comment that:
There are many other points of common interest between data mining and mainstream statistical analysis, points that one would cover in a course on statistical regresstion and classification modelling. Variable selection is as much or more an issue in data mining as in mainstream statistical analysis. Depending on how results are to be used, the confounding of effects of variables may be a serious problem for interpretation.
Here is a list of emphases that come through from the proponents of Data Mining and Knowledge Discovery in Databases. My responses, which are in italics, are a form of summary of the points that I have made earlier in the paper:
I am grateful to members of the Friday morning Canberra Applied Statistics group for helpful comments. Andreas Ruckstuhl read a draft and made a number of comments which led to substantial improvements. He is not of course responsible for what I have made of his comments.
Begg, C., Cho, M., Eastwood, S., Horton, R., Moher, D., Olkin, I., Pitkin, R.,Rennie, D., Schulz, K. F., Simel, D., and Stroup, D. F. 1996. Improving the Quality of Reporting of Randomised Controlled Trials: the CONSORT Statement. Journal of the American Medical Association 276: 637 - 639.
Beveridge, W. I. B., 3rd. edition 1957. The Art of Scientific Discovery. Vintage Books, New York.
Chassin, M. R., Hannan, E. L. and DeBuono, B. A. 1996. Benefits and hazards of reporting medical outcomes publicly. New England Journal of Medicine 334: 394-398.
Jessup, A. J. and Baheer, A. 1990. Low-temperature storage as a quarantine treatment for kiwifruit infested with Dacus tryoni (Diptera: Tephritidae). Journal of Economic Entomology 83: 2317-2319.
Elder, J. and Pregibon D. 1996. A statistical perspective on Knowledge Discovery in Databases. In Fayyad, U. M., Piatetsky-Shapiro, G., Smyth, P. and Uthurusamy, R.: Advances in Knowledge Discovery and Data Mining, pp. 83-113. AAAI Press/MIT Press, Cambridge, Massachusetts.
Fayyad, U. M., Piatetsky-Shapiro, G. and Smyth, P. 1996. From data mining to knowledge discovery: An overview. In Fayyad, U. M., Piatetsky-Shapiro, G., Smyth, P. and Uthurusamy, R.: Advances in Knowledge Discovery and Data Mining, pp. 1-34. AAAI Press/MIT Press, Cambridge, Massachusetts.
Friedman, J. H. 1997. Data Mining and Statistics. What's the Connection? Proc. of the 29th Symposium on the Interface: Computing Science and Statistics, May 1997, Houston, Texas.
Heard et al. 1991. Dose-mortality relationships for eggs and larvae of Bactrocera tryoni (Diptera: Tephriditae) Immersed in Hot Water. Journal of Economic Entomology 84: 1768-1770.
Jessup, A. J. and Baheer, A. 1990. Low-temperature storage as a quarantine treatment for kiwifruit infested with Dacus tryoni (Diptera: Tephritidae). Journal of Economic Entomology 83: 2317-2319.
Jorgensen, M. and Gentleman, R. 1998. Data mining. Chance 11: 34-39 & 42.
King, D. A. and Maindonald, J. H. 1999. Tree architecture in relation to leaf dimensions and tree stature in temperate and tropical rain forests. Journal of Ecology, to appear.
Mackinnon, M. J. and Glick, N. 1999. Data mining and knowledge discovery in databases an overview. Australianm and New Zealand Journal of Statistics 41: 255-275.
Maindonald, J. H. 1999. New approaches to using scientific data statistics, data mining and related technologies in research and research training. Occasional Paper 98/2, The Graduate School, Australian National University.
Maindonald, J. H. and Finch, G. R. 1986. Apple transport in wooden bins. New Zealand Journal of Technology 2: 171-177.
McPherson, K. 1990. Why do variations occur? In Anderson, T. F. and Mooney, G., eds.: The Challenges of Medical Practice Variations, pp.16-35. Macmillan Press, London.
McPherson, K., Strong, P. M., Jones, L. and Britton, B. J. 1982. Small area variations in the use of common surgical procedures: An international comparison of New England, England and Norway. New England Journal of Medicine 307: 1310-1314.
Ng, M. K., Huang, Z., and Hegland, M.. 1998. Data-mining massive time series astronomical data sets - a case ctudy. Second Pacific-Asia Conference on Knowledge Discovery in Data Bases, PAKDD98, 1998, pages 401-402.
Porter, R. 1997. The Greatest Benefit to Mankind. Harper Collins, London.
Ripley, B. D. 1996. Pattern Recognition and Neural Networks. Cambridge University Press, Cambridge.
Sackett, D. L., Richardson, W. S., Rosenberg, W. M. C. and Haynes, R. B. 1997. Evidence-Based Medicine. Churchill Livingstone, New York.
Sackett, D. L. and Oxman, A. D., eds. 1994. The Cochrane Collaboration Handbook. Cochrane Collaboration, Oxford.
Sales, F., Paulaud, D., and Maindonald, J. 1997. Comparison of eggs and larval stage mortality of three fruit fly species (Diptera: Tephriditae) after immersion in hot water. Pp. 247-250 in Allwood, A. J. and Drew, R. A. I., eds., Management of Fruit Flies in the Pacific. Australian Centre for International Agricultural Research, Canberra.
Selfridge, P. 1996. In from the start. IEEE Expert 11: 15-17 and 84-86.
Stigler, S. M. 1977. Do robust estimators work with real data. Annals of Statistics 54: 1075.
Taubes, G. 1998. The (Political) Science of Salt. Science 281: 898-907 (14 August).
Warhaft, S., ed. 1965. Francis Bacon. A Selection of His Works. The Macmillan Company of Canada.