Adaptive Optics
Adaptive optics is an emerging field with applications in areas as diverse as astronomy, opthalmology, 3D imaging, retinal imaging (see Figure 1), laser material processing and military imaging. Light is distorted by the medium through which it travels, adaptive optics attempts to compensate for that distortion to produce more clear and detailed images.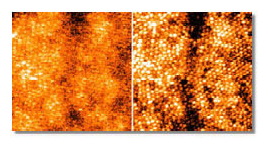
retina.png
Images of the retina using conventional optics and adaptive optics. The images were originally taken from http://www.nsf.gov/od/lpa/news/media/01/fsjan01aas.htm. Updated information is available at http://cfao.ucolick.org/pgallery/vision.php.
The specific application we are interested in is astronomy. The image resolution that may be obtained by traditional telescopes is limited due to factors such as interference by the earths constantly changing atmosphere. New telescopes based on adaptive optics compensate for the distortions by calculating the aberrations in the wave-front and changing the shape of deformable mirrors to correct blurring. The improvement in the quality of the image is demonstrated by the results in Figure 2 and Figure 3.
titan3.png
Titan (Saturn's largest moon). More detail can be seen in the images obtained by the Keck telescope through the use of adaptive optics. http://cfao.ucolick.org/ao/why.php.
galaxy_with_and_without_ao.png
The nuclear region of the nearby galaxy NGC 7469, with and without adaptive optics. http://cfao.ucolick.org/ao/why.php.
The wave-front is not usually measured directly, rather its shape is inferred by its effects on intensity measurements. The traditional approach to wave-front reconstruction is based on the Shack-Hartmann test, which has a high computational cost for large images. More recent papers on this topic focus on the use of the irradiance transport equation (which is also called transport of intensity equation in some references):
∇⊥ .(I(r⊥, z) ∇⊥ φ(r⊥, z)) = −k ∂z I(r⊥, z),
where I is the intensity measurements and φ is the wave-front phase.
The numerical solution of diffusion type equations has been studied extensively, yet there is no recognised technique for solving the irradiance transport equation. Part of the reason is due to the experimental set-up. There is also a more subtle, but important, issue; and that is the effect of noise in the intensity measurements.
Very accurate, robust and fast calculations of the wave-fronts are required to control these systems and to return high resolution images in real time. The only way to achieve this goal is to use techniques that are at the forefront of both the mathematical and computer sciences. These tools include the choice of appropriate basis functions that can be calculated quickly and can handle the noise present in experimental data. We also plan to address issues where algorithms and architecture interact, namely the efficient use of memory systems for obtaining high performance.


File translated from TEX by TTH, version 3.67.
On 23 Oct 2005, 20:12.