Prolonged Plasma Fluid Simulations

Prolonged Plasma Fluid Simulations
Work with Ryusuke Numata and Rowena Ball

Description

The focus of numerical simulation of turbulent flows has shifted in recent years from observing contours of the stream function and derived quantities in specified geometries to mining the resulting data sets for correlations, coherent structures, patterns, and instabilities that can inform us on the physics that governs turbulent transport. To design or predict the behaviour of turbulent flows we also need data sets for ranges of tunable parameters of practical interest. For these purposes the ability to compute prolonged time series is essential. By "prolonged" we mean time series from which meaningful statistics on patterns at all scales of the motions can be extracted, with the constraints of being computable on available processors in practicable real time, such as that of a student project. The major quandary is how to choose a numerical method that can allow long time steps and does not pollute the results with numerical instabilities.

Fluid simulations of turbulent fusion plasmas have often driven the development of improved numerical algorithms and methods, for the general reason that such systems present many interesting and relevant physics and engineering problems in regimes of limited experimental accessibility. A few representative examples are the gyrokinetic particle simulations in [7], the improved parallelisation algorithms in [10], and the emphasis in [11] on numerical methods that self-consistently reproduce the main physics processes such as zonal flow-turbulence interactions.

In magnetic fusion plasmas zonal flows are low frequency coherent structures of the electrostatic potential¹ that are generated by the characteristic small scale drift wave turbulence [5]. Zonal flows play an important role in quenching turbulence and consequent anomalous transport that, left unchecked, thwarts confinement and control of the plasma. An intensively investigated manifestation of this effect is the phenomenon of confinement transitions, characterised by rapid onset (abatement) of sheared mass flows concomitant with suppression (growth) of high wavenumber turbulence [2,6,12].

Recent work [8] in simulating drift wave turbulence described by the Hasegawa-Wakatani equations [4] has indicated that the generation of zonal flows and resulting transport suppression occurs as a bifurcation scenario, in which turbulent kinetic energy, fed by a density gradient, builds up to a critical level before the rapid onset of zonal flow structuring. Investigations of both the build-up to criticality and the subsequent flow structure require excavation and analysis of prolonged time series, for several reasons: 1) Close to an instability a perturbed dynamical system typically takes a long time to return to equilibrium - this is a consequence of the asymptotic nature of linear stability theory. 2) The quality of time series near a bifurcation is also important, in that simply decreasing the sampling rate to achieve long series usually gives spurious results. 3) Prolonged time series are also necessary to extract patterns and structure from the data. Most techniques of mining spatiotemporal data work poorly with short data sets in which the errors are large. 4) We would like a picture of the dynamics over the parameter space. However, the computational cost of prolonged simulations near instabilities, in structured regimes, and for ranges of parameters is still prohibitive.

The Hasegawa-Wakatani model [4] was designed to extend the one field Hasegawa-Mima model [3] for drift wave turbulence in magnetic fusion plasmas to include the physics of electron motions parallel to the background toroidal magnetic field. Due to the strong magnetic field, plasma dynamics in the plane perpendicular to the magnetic field is well separated from the dynamics in the parallel direction. However, the parallel motion brings about additional physics by coupling the flow field given by the electrostatic potential φ with the density r in the Hasegawa-Wakatani equations. The equations in a two-dimensional domain are given by

∂

∂t

∇² φ + [φ, ∇² φ]

α(φ-r) - β_φ ∇^2(p+1)φ

(1)

∂

∂t

r + [φ, r]

α(φ-r) - κ

∂φ

∂y

- β_r ∇^2p r.

(2)

where φ = φ(x, y, t), r = r(x, y, t), and ∇²=∂²/∂x² + ∂²/∂y² is the two-dimensional Laplacian. The Poisson bracket [.,.] defined by

[f,g] =

∂f

∂x

∂g

∂y

∂f

∂y

∂g

∂x

gives the convective derivative. The parameters, α, β_φ, β_r and κ are all non-negative. Physically, the κ term feeds energy to the system, while the energy is dissipated by the parallel resistivity (α) and hyper-diffusions (β_φ, β_r). The Hasegawa-Wakatani model includes interesting physics although it is too simplified to capture realistic dynamics occurred in fusion plasmas. The model describes anomalous edge transport due to drift wave turbulence and self-generation of coherent macroscopic flow structures. Moreover, an interplay between the turbulence and the large-scale flows leads to complex bifurcation phenomena. We refer the reader to [1,4,8,9] for more discussions on the physical interpretation of the system.

Results

A Fortran 90 program has been written to simulate the Hasegawa-Wakatani model. Results for periodic and zero boundary conditions are available.

Results for p = 2, β_r = β_&phi = 0.0000001, κ = 1.0, α = 1, 0 ≤ t ≤ 1000 and computational grid size = 256 × 256

Potential	Density	Vorticity

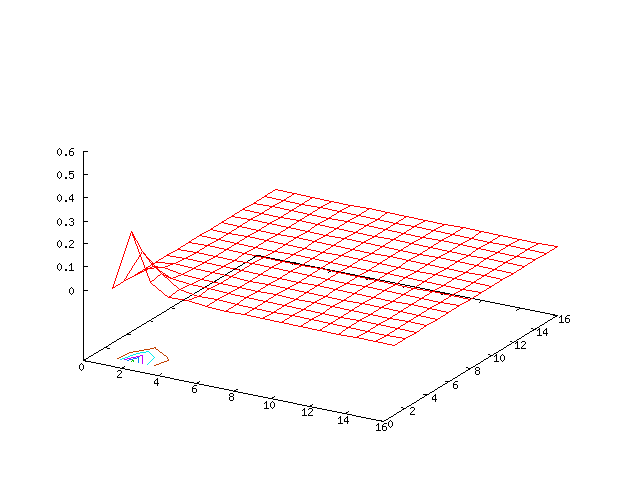
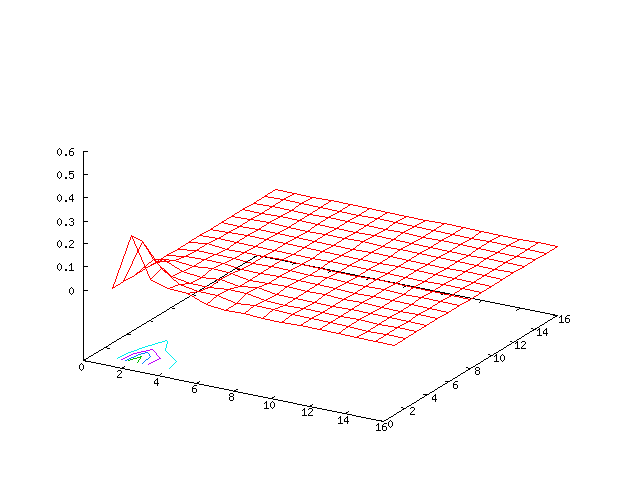
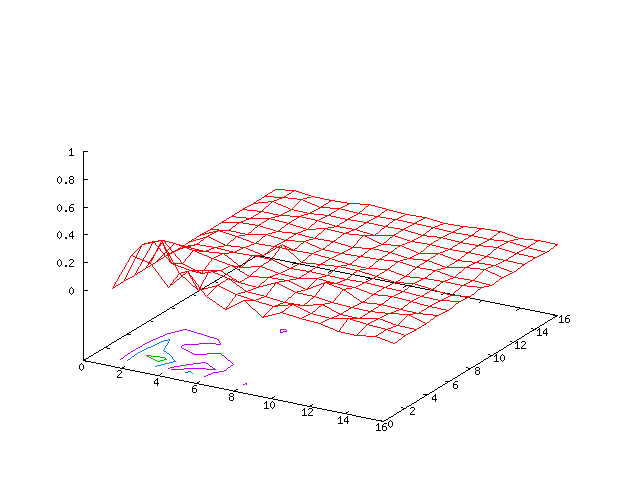
Potential	Density	Vorticity

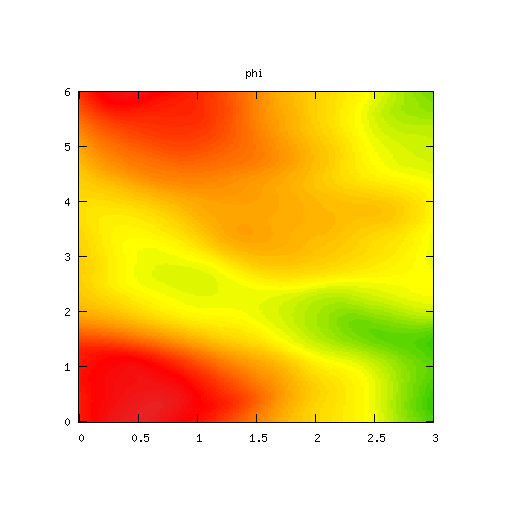
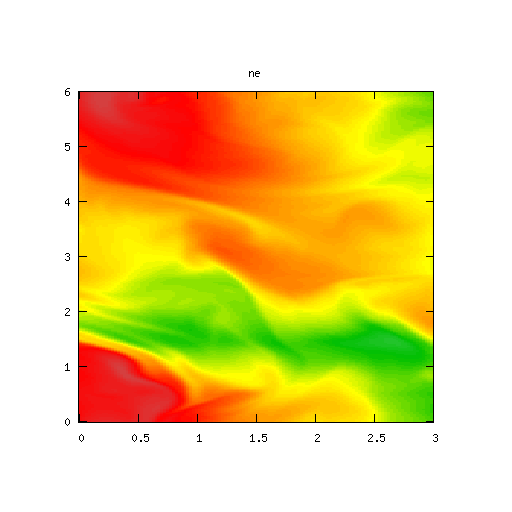
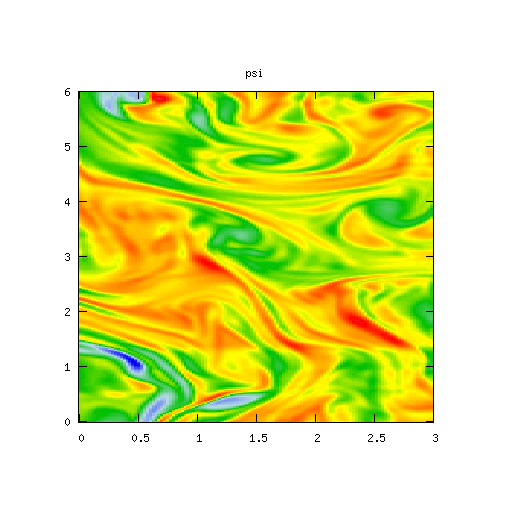
Publications

L. Stals, R. Numata, and R. Ball. Stability analysis of time stepping for prolonged plasma fluid simulations. SIAM Journal on Scientific Computing, 31(2):961-986, 2008.
L. Stals. Nonlinear Analysis of the Solutions of the Hasegawa-Wakatani Equations. Preprint: arXiv:1107.0112

References

[1]: S. J. Camargo, M. K. Tippett, and I. L. Caldas, Nonmodal energetics of resistive drift waves, Phys. Rev. E, 58 (1998), pp. 3693-3704.
[2]: J. W. Connor and H. R. Wilson, A review of theories of the L-H transition, Plasma Phys. Control. Fusion, 42 (2000), pp. R1-R74.
[3]: A. Hasegawa and K. Mima, Pseudo-3-dimensional turbulence in magnetized nonuniform plasma, Phys. Fluids, 21 (1978), pp. 87-92.
[4]: A. Hasegawa and M. Wakatani, Plasma edge turbulence, Phys. Rev. Lett., 50 (1983), pp. 682-686.
[5]: W. Horton, Drift waves and transport, Rev. Mod. Phys., 71 (1999), pp. 735-778.
[6]: J. Hugill, Edge turbulence in tokamaks and the L-mode to H-mode transition, Plasma Phys. and Control. Fusion, 42 (2000), pp. R75-R91.
[7]: Z. Lin, T. S. Hahm, W. W. Lee, W. M. Tang, and R. B. White, Turbulent transport reduction by zonal flows: Massively parallel simulations., Science, 281 (1998), pp. 1835-1837.
[8]: R. Numata, R. Ball, and R. L. Dewar, Bifurcation in electrostatic resistive drift wave turbulence, Phys. Plasmas, (2007). accepted for publication.
[9]: T. S. Pedersen, P. K. Michelsen, and J. J Rasmussen, Resistive coupling in drift wave turbulence, Plasma Phys. Control. Fusion, 38 (1996), pp. 2143-2154.
[10]: T. D. Rognlien, X. Q. Xu, and A. C. Hindmarsh, Application of parallel implicit methods to edge-plasma numerical simulations, J. Comput. Phys., 175 (2002), pp. 249-268.
[11]: B. D. Scott, Computation of turbulence in magnetically confined plasmas, Plasma Phys. Control. Fusion, 48 (2006), pp. B277-B293.
[12]: P. W. Terry, Suppression of turbulence and transport by sheared flow, Rev. Mod. Phys., 72 (2000), pp. 109-165.

Footnotes:

¹The stream function φ for a two dimensional flow, defined by u=∇×(φe_z) where u is the velocity vector in the x-y plane, is identified with the electrostatic potential φ in fusion plasmas where the flow is primarily given by the E×B drift; u_E×B=∇×( -φ/B₀e_z).

File translated from T_EX by T_TH, version 3.67.
On 21 Jan 2008, 11:36.