POLYNOMIAL CHAOS
Quantifying Uncertainty
Sample menu:
Tutorial Menu
RESULTS
In this section we present the numerical results of Hermite Chaos applied to the linear ODE defined on
the previous page. Here we assume that the growth parameter
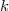has a Gaussian distribution with mean
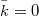and standard deviation 
.
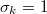The deterministic solution to the linear ode is well known
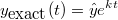
and consequently we can calculate the exact stochastic mean and variance. The exact stochastic mean is
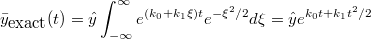
where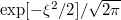 
is the PDF of the univariate random variable
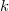and 
and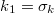
are the non-zero coefficients of the gPC expanion of 
.
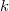Similarly the exact variance is
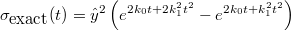
The figure below plots the convergence of the relative error in the mean and variance of
the stochastic linear ODE at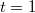 
. The relative error in both the mean and variance
decreases exponentially with increasing 
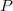. However the variance of the gPC
approximation converges more slowly than the mean.
