Sample menu:

Tutorial Menu

GENERAL PROCEDURE OF STOCHASTIC GALERKIN METHODS

The implementation of gPC involves the following seven steps. (I) Identify the sources of uncertainty in the model in question. (II) Choose independent random variables with appropriate PDFs to represent these sources of uncertainty (III) Construct a generalised Polynomial Basis. (IV) Use this basis to construct a gPC expansion of the sources of uncertainty - initial conditions, parameters etc. (V) Substitute the gPC expansions into the governing equations. (VI) Perform a Galerkin projection to transform the stochastic equation into a set of coupled deterministic equations. (VII) Solve the resulting system of equations with appropriate numerical methods.

Consider the general stochastic differential equation

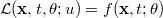
where the random process 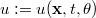is the solution, 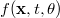is the source term and 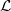is a linear or nonlinear operator. The random parameter 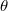represents uncertainty introduced by initial or boundary conditions, rate parameters, system properties, etc. Using the Generalised Polynomial chaos expansion we can write 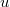as

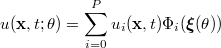
Here we have restricted the infinite sum to a finite summation involving 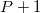expansion terms. The total number of terms depends on the number of dimensions 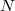of the random multivariate parameter 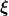and the highest order 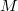of the polynomials 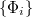set according to the required accuracy

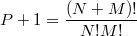
To obtain the best rate of convergence the polynomials are chosen with the matching random distribution. Orthogonal polynomials can also be constructed numerically to deal with arbitrary probability measure [Xiu 2002 1.]. Once an appropriate basis has been chosen the truncated gPC expansion is substituted into the governing equation to obtain

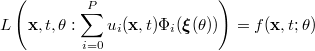
A Galerkin projection is then used to project the above equation onto the random space spanned by the polynomial basis. This is performed by successively evaluating the inner-product of the above equation with each basis element ,

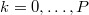
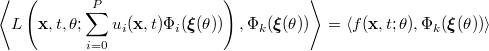
Utilizing the orthogonality condition yields a set of 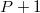coupled deterministic equations. This system can then be solved using appropriate numerical methods. Once the gPC approximation of the solution is obtained various statistical measures can be calculated. For instance, the mean 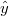and variance 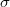of the gPC approximation are given by

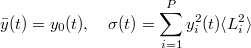
Notice that the mean is simply the first term in the gPC expansion of the solution 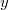and that the mean is absent from the summation used to calculate the variance.

[ Continue ]