POLYNOMIAL CHAOS
Quantifying Uncertainty
Sample menu:
Tutorial Menu
GENERALISED POLYNOMIAL CHAOS EXPANSIONS
To achieve faster convergence rates for non-Gaussian inputs Xiu and Karniadakis [Xiu 2002] developed a generalisation of Wiener's Chaos known as Wiener-Askey polynomial chaos or generalized Polynomial Chaos (gPC). This scheme utilises the Askey-scheme class of orthogonal polynomials, of which Hermite polynomials are a subset. Each set of orthogonal polynomials in the Askey-scheme have a different weighting function in their orthogonality relationship. In some cases these weighting functions are identical to the probability of certain discrete and continuous random distributions. Some of the Askey polynomials and the random distributions satisfying this property are shown in the Table. The correct choice of random distribution polynomial result in optimal convergence.
| Random Distribution | Askey Polynomial | Support | |
|---|---|---|---|
| Continuous | Gaussian | Normalised Hermite Polynomials |  |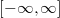
| Uniform | Legendre Polynomials |  |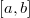
|
| Gamma | Laguerre Polynomials |  |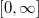
|
| Beta | Jacobi Polynomials |  |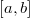
|
| Discrete | Poisson | Charlier Polynomials |  |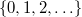
| Negative Binomial | Miexner Polynomials |  |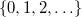
|
| Binomial | Krawtchouk Polynomials |  |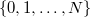
|
| Hypogeometric | Hahn Polynomials |  |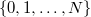
Under Generalised Polynomial Chaos the general second-order random process
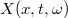is now represented by
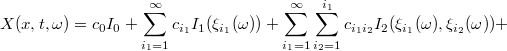
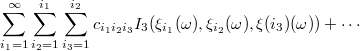
where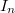 
is the Wiener-Askey polynomial of order 
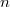. The defining difference
between Wiener's Hermite approximation (\ref{eq:expanded_weiner_chaos}) and the
gPC expansion (\ref{eq:expanded_gpc}) is that the orthogonal polynomials 
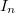are
no longer restricted to be Hermite polynomials. Rather the orthogonal polynomials
can assume any polynomial proposed used by the Askey-scheme. To promote fast rates
of convergence, the type of polynomial selected is based upon the distribution of
the independent variables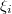 
. Refer to Table \ref{tab:variable_polynomial}.
It assumed that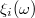 
are independent random variables with probability
density functions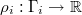 
with bounded ranges
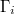. Under this assumption the joint density of 
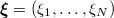is
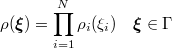
defined over the support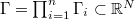 
We can expect each type of gPC to converge to any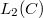 
functional in the
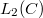sense in the corresponding Hilbert functional space as a generalized
result of the Cameron-Martin theorem [Cameron 1947]. For example, Ogura
[Ogura 1972] shows that any nonlinear functional of a Poisson process with
finite variance can be developed in terms of a Poisson-Wiener integral, defined
using multivariate Charlier polynomials, in a close analogy to the Wiener-Hermite
expansion.
For convenience Eq. (\ref{eq:expanded_gpc}) can be rewritten as
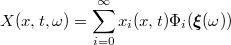
Here we have performed a a simple re-ordering by counting polynomials of lower
order first.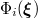 
forms a complete orthogonal basis, so
that
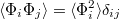
where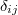 
is the Kroneker delta and 
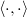is the inner
product in the Hilbert space determined by the support of the random variable
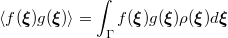
The weighting function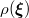 
is determined by the type of
random variable used. Refer to Table \ref{tab:variable_polynomial}. There is a
one-to one correspondence between the polynomials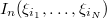 
and 
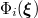. For example, the two-dimensional Hermite chaos in
the fully expanded form of Eq. (\ref{eq:expanded_gpc}) is
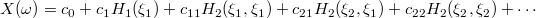
and in the simplified form of Eq. (\ref{eq:simple_gpc})
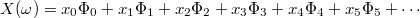
[ Continue ]