POLYNOMIAL CHAOS

Quantifying Uncertainty

Sample menu:

• Introduction
• Home Page
• Applications
• Publications
• Tutorial
• Research Positions
• Contacts

Tutorial Menu

• Introduction
• Problem Definition
• Representing Stochastic Processes
  • Polynomial Chaos Expansions
  • Generalised Polynomial Chaos Expansions
  • Karhunen-Loeve Expansions
• Stochastic Galerkin Methods
  • General Procedure
  • Example
  • Results
• Stochastic Collocation Methods

PROBLEM DEFINITION

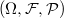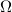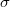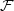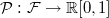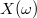To quantify the uncertainty in a system of differential equations we adopt a probabilistic approach and define a complete probability space . This space consists of an event space , comprising of possible outcomes , a -algebra and a probability measure . Utilising this framework the uncertainty in a model can be introduced by representing the model input data as random fields. . These random fields 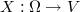are mappings from the probability space into a function space 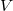. 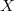If is a random variable then 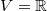and 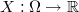. Alternatively if 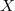is a random field or process, such as a Wiener process, 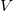is a function space over a temporal and/or spatial interval.

Governing Equations

Consider the general differential equation defined on a 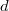-dimensional bounded domain ()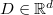

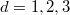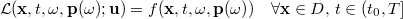
where 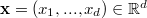, 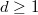are the coordinates in 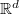, 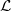is a linear or non-linear differential operator, 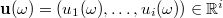, 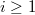are the unknown solution quantities and 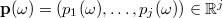, 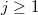are the input data, either parameters or stochastic processes, characterising the governing equations. Note that we have omitted the equation for the boundary and initial conditions for convenience.

We are interested in finding the stochastic solution 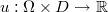such that for 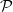-almost everywhere 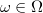, equation~(\ref{eq:stochastic_general_differential_eq}) holds.

[ Continue ]

[ Back to top ]

2008 John Jakeman