Sample menu:

Tutorial Menu

A SIMPLE EXAMPLE

This section investigates the performance of generalised Polynomial Chaos when applied to the simple one-dimensional linear stochastic differential equation

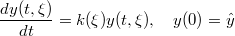
The above equation is a univariate (one dimensional) second order stochastic process which describes the growth of a population 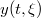subject to a random growth rate 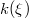. Here we will restrict our attention to Gaussian and Uniform distributions of 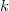. This example was previously documented by Lucor 2004.

Following the general procedure we begin by utilising the truncated gPC expansion to expand the solution 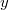and the random variable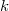

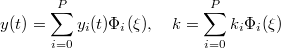
Using Hermite and Legendre Chaos 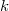can be represented exactly by a first order expansion

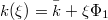
where 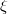is Gaussian with mean zero and unit variance when implementing Hermite Chaos or uniformly distributed in 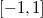when invoking Legendre Chaos. These expansions can then be substituted into the governing equations to obtain

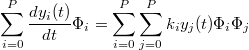
A Galerkin projection is then used to project the above equation onto the random space spanned by the polynomial basis. This is performed by successively evaluating the inner-product of the above equation with each basis element 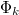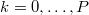. Then exploiting the orthogonality relation we obtain

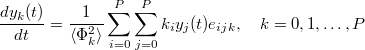
where . The values of 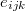and 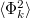can be obtained analytically.

Now we have a set of 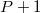coupled deterministic equations which can be solved using appropriate numerical methods. Once the simulation is completed the mean 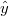and variance 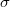in the gPC solution can be found.

In the cases where an analytical deterministic solution exists 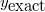, as it does for or example we can also determine the exact stochastic mean 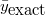and variance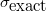

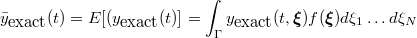
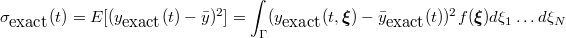
and

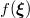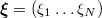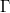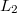Here is the multi-dimensional probability density function of the multivariate random variable defined over the support . These values can the be used to approximate the error in the gPC solution. In the following sections we investigate the relative error in the mean and variance, given respectively by

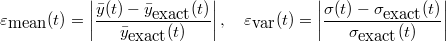
[ Continue ]